
a background article by:
Michelle Kathleen Hall-Wallace
Department of Geosciences
1040 East Fourth Street
University of Arizona
Tucson, Arizona 85721-0077
Dr. Hall-Wallace is now at:
Science Education Solutions,
4200 West Jemez Road, Suite 301
Los Alamos, New Mexico 87544
Put on the web with permission of Michelle Hall-Wallace (University of Arizona) and the Journal of Geoscience Education (published by the National Association of Geoscience Teachers)
Theoretical Models for Earthquake Prediction
Data Analysis and Evaluation of the models
Modeling fault behavior with a simple slider-block apparatus can provide students with valuable insight into the difficulty of earthquake prediction and the complex behavior of Earth systems. I have developed an open-ended activity in which students are challenged to design an experiment that models fault behavior and to determine which variables in the earth might affect the number or magnitude of earthquakes that occur. I have used the activity with secondary-school science teachers and their students, but it is also appropriate for undergraduate geoscience majors. Students are provided with materials to construct a fault model, but few instructions are given. Their investigations are guided by curiosity and a few key questions that I suggest they investigate in their experiment. Working in groups, the students design the apparatus, develop an experimental procedure, determine what to measure, and analyze their data. In the process they learn how science is done and increase their level of scientific literacy (NRC, 1996).
The activity provides many opportunities for graphing and basic statistical analysis. In addition, students are introduced to the complexity of scientific problems and to the value and limitations of models. Data collected from a simple mechanical model correspond will wit the observed behavior of real faults and can be interpreted in terms of basic models for earthquake prediction.
Keywords: Apparatus; earth science – teaching and
curriculum; earth science – teacher education; education
– geoscience; education – undergraduate; geophysics
– seismology; mathematical geology; pseudoscience.
At 6:00 am on January 17, 1994, disaster struck southern California in the form of an earthquake that originated deep beneath the Santa Susana Mountains. Slippage occurred on a fault and the resulting earthquake damaged buildings and highways, ruptured gas lines, and created chaos in the largest metropolitan area in the western US. Every news organization had special reporters on the scene. Pictures of damage and fires as well as interviews with distraught victims formed a steady parade across television screens. Even the most jaded students were fascinated with the awesome power of the earth.
Earthquakes constitute a wonderful tool for motivating students to investigate and understand the behavior of the earth. "What causes earthquakes?", "What determines their magnitude?", and "Can we predict when the next earthquake will occur?" are questions frequently asked. The mystery of when and where the next "Big One" will occur is a pressing and interesting question for the public. Unfortunately, most of the recent short-term earthquakes predictions were based on lost-cat reports in newspapers or planetary tidal forces and weather (for example, Iben Browning’s prediction for a big New Madrid quake; see Coleman and Soellner, 1995; Picard, 1995), rather than on sound science. The fact that these predictions can attract intense media attention reveals much about the scientific literacy of the public and the need for our students to know and use scientific methods and reasoning.
One of the greatest challenges to seismologists is to be able to predict earthquakes with enough precision to minimize loss of life and economic hardship. In an ideal world, we would know where all active faults lie, when they will rupture, and the magnitude of the next earthquake expected. Earthquake prediction is successful when it can routinely provide accurate information on time, location, and size of future earthquakes. Long-term predictions affect urban planning decisions. Intermediate predictions promote emergency preparedness and heighten awareness. Successful short-term predictions lead to evacuation orders that can save lives. Seismologists can determine probabilities of rupture for particular faults or fault systems, but these probabilities are only as good as our knowledge of past earthquakes, long-term rates of fault movement , and local fault interactions. Well documented historical accounts, geologic and geodetic studies, and modern earthquake recordings are used to develop some understanding of a particular fault’s behavior. One of the problems encountered is that we rarely have more than one or two earthquake cycles in the historical record.
In the United States, improved understanding of fault behavior, responsible urban planning, and advances in building construction have greatly reduced the threat to life from earthquakes, yet more could be done to reduce our exposure to their hazards . Our growing understanding of the mechanics of earthquakes and the behavior of the earth will continue to bring us closer to safety. To help students understand the behavior of faults and the challenges of earthquake prediction, I developed an activity which allows students to investigate the mechanics of faults, hazards are more statistical then deterministic in their occurrence. In the course of doing the exercise, the students create models of faults based on the mechanics of earthquake slip to investigate and understand some of the variables affecting fault-rupture patterns and frequency.
The activity challenges students to design their own experiments,
explore the interdependency of variables, and analyze data in
an open-ended problem. Inquiry-based activities promote scientific
literacy by teaching students to "ask, find, or determine
answers to questions derived from curiosity about everyday experiences"
(NRC, 1996, p. 22). I use the activity in an Earth Hazards course
for secondary-school earth science and physics teachers and have
also worked with secondary-school teachers on using the activity
in their classrooms. The activity is also appropriate for an undergraduate-level
geology or geophysics class. In this paper I will describe the
science background I cover in preparing students for the activity;
then I will discuss the experiment itself.

In 1910, Harry Reid proposed the "elastic rebound theory" of earthquake origins based on field observations of the effects of the 1906 San Francisco earthquake (Reid, 1910). Prior to 1906, limited field observations had left scientists debating whether earthquake shaking caused ground surface breakage or ground surface breakage caused earthquake shaking. Reid carefully studied ground breakage near the San Andreas fault and geodetic data away from the fault after the 1906 earthquake and formulated the theory that crustal stresses resulting from large-scale shearing motions cause elastic strain to accumulate in the vicinity of faults. When the strain accumulation reaches a critical threshold imposed by the material properties of the rock and the fault surface, abrupt frictional sliding occurs, releasing some of the elastic strain energy (Figure 1). Much of the strain energy released is used in heating and fracturing of rock, but a portion is converted to seismic waves. After an earthquake, elastic strain begins to accumulate again to accommodate regional forces. This process leads to many cycles of strain accumulation and release over the life of a fault.
The dynamics of fault rupture are complex, but general fault behavior can be explained with a simple model in which slip promotes fault weakening. Fault slip occurs in three stages: 1) initiation of sliding on a small portion of the fault, 2) growth of the slip surface, and 3) termination of slip and fault healing (Scholz, 1990). Earthquakes occur on preexisting faults operating in a "stick-slip" mode. Earthquakes are "slip" episodes; they are followed by periods of no slip ("stick"), during which elastic strain increases away from the fault. Although some growth of the fault may occur with each earthquake, we can generally assume that for large earthquakes (M>6) the faulting process primarily involves repeated breaking of the same fault segment rather than creation of a new fault surface (Walsh and Watterson, 1988). Measurements of strain accumulation for several well documented large earthquakes indicate that the crust cannot accumulate elastic strain much larger than 10^-5 without failure (Kanamori, 1977).
The crust of the earth is not homogeneous and several variables affect the behavior of faults. Brace and Byerlee (1967) and Byerlee (1967) showed that friction on existing fault surfaces is independent of rock type but that factors such as gouge, asperities and fluid pressure can significantly affect the level of stress buildup prior to an earthquake. Asperities, or protrusions on the fault, act like welded contacts between the sides of the fault. Younger faults have rougher surfaces with more asperities. As a fault repeatedly ruptures, the asperities can be worn down, creating fault gouge and smoothing the fault. The gouge material often decomposes to a fine clay and forms a thin layer which "greases" the fault for easier sliding. Fluids can also facilitate slip by reducing the normal stress on the fault.
Earthquakes have been triggered by pumping water into the subsurface in areas of nuclear waste disposal, mining, and oil production (Evans, 1996). Earthquakes are also triggered when man-made structures, such as water reservoirs or rock quarries, increase or decrease the overburden stress on a region (Simpson and others, 1988). The change in load may increase the stress on an underlying fault and cause rupture. Marone and Scholz (1988) showed that small earthquakes generally occur at shallow depths where the rocks are weaker and the lithostatic stress is lower. At shallow depths it is difficult to build up high stresses; therefore, the earthquakes that do occur have smaller slip displacements. At greater depths in the crust, larger earthquakes are observed. The higher lithostatic stress at these depths requires higher shear stresses to break fault segments, and when higher shear stress is reached, a larger earthquake can be generated (Wallace and Kemeny, 1992; Wallace and Wallace 1993).
Reid’s elastic rebound theory combined with our knowledge
of plate tectonics suggests that we might someday be able to predict
earthquakes. The observation that some faults fail with quasi-periodic
behavior is fundamental for earthquake prediction and hazard mitigation.
Theoretically, if plate motions are steady, strain accumulation
will increase steadily and slip will occur at regular time intervals;
the amount of time between slip episodes is called the recurrence
interval. There are three basic models for earthquake prediction:
1) the characteristic earthquake, 2) the time-predictable earthquake,
and 3) the slip-predictable earthquake (Lay and Wallace, 1995).
Each model is based on the history of stress accumulation and
relaxation during an earthquake cycle (Figure 2). In the characteristic
earthquake model (Figure 2a), shear stress builds on a fault to
the level of the fault strength, t1. When the shear stress reaches
t1, the fault ruptures and the shear stress is reduced to a level
equal to the friction on the fault, t2. The amount of slip on
the fault is the same for each earthquake and the recurrence interval
is constant over time. Unfortunately, characteristic earthquake
behavior is not commonly observed in nature because the model
assumes that plate motions are steady and fault friction and fault
strength are constant. However, a section of the San Andreas fault
near Parkfield, California may be one example of a fault that
follows the characteristic earthquake model. This fault segment
has had at least five M>6 earthquakes with a mean recurrence
interval of 22 years (Bakun and Lindh, 1985) since 1857. There
is some variability in the recurrence interval, but studying this
characteristic behavior may be the first step towards understanding
fault behavior.

The time-predictable model (Figure 2b) assumes that fault strength is constant and that the fault will always rupture when the shear stress reaches the level of t1. However, slip on the fault can vary with each rupture. This model assumes that a large slip on the fault will reduce the level of shear stress more than a small slip. Thus, after a large slip it will take longer for the shear stress to build to the level of t1, assuming steady plate motions. Knowing the amount of slip during the past earthquake, the time-predictable model allows prediction of the time of the next earthquake. The Calaveras fault near San Francisco Bay, California appears to have time-predictable behavior over at least the short time window of observation from 1962-1977 (Bufe and others, 1977). The cumulative amount of slip is linear over time even though the amount of slip during any one earthquake varies.
In the slip-predictable model (Figure 2c), the fault does not rupture at the same shear stress, t1, each time. Rather, an earthquake always reduces the shear stress on the fault to t2, the level of the fault friction. This model cannot be used to predict when rupture will occur, but it can be used to predict the magnitude of the earthquake that would occur at any given time. After an earthquake, stress on the fault will increase at a constant rate from t2. The potential fault slip at any time is proportional to the shear stress on the fault. Thus, if the time of the last rupture is known, the shear stress on the fault and the potential displacement can be determined at any particular time.
The Mechanical Model
Students can create a mechanical model of stick-slip behavior in the lab using a slider-block configuration like that shown in Figure 3. A brick or heavy wood block represents one side of a horizontal fault while the other side is a flat, six-foot board. One or both sides of the "fault" can be covered with sandpaper to create surfaces with higher friction. Under a microscope, the contact between the brick and sandpaper would look very irregular. The grains of sandpaper grit are the contact points that act as asperities on the fault. Attached to the brick is a short bungee cord, which is itself attached to non-stretching rope coiled on a hand crank or winch. A spring scale can be added to the model to measure the force at which the "fault" initiates rupture (fi) and the force when it comes to rest (fr). We use a metric ruler to measure the amount of slip during each rupture and use the slip as a proxy for magnitude, assuming that larger slip corresponds to larger magnitude.
The change in force from the initiation of slip until the block
is at rest (fr-fi) can be used to calculate the change in stress,
or stress drop, associated with the fault-slip event. Stress is
calculated as force/unit area. In our mechanical model, the fault
area (A) is equal to the area of the brick in contact with the
board. Thus, shear stress on the fault at rupture (t1) and at
rest (t2) are equal to fi/A and fr/A, respectively. The difference
between the shear stress just before the slip event (t1) and just
after the slipping has ceased (t2) is known as the stress drop.
Because the area of the fault does not change in our mechanical
model, the values of fi and fr directly correlate with t1 and
t2 as used in the theoretical models for earthquake prediction
(Figure 2). In our analysis of the data, we use this correlation
to compare the models for earthquake prediction to the data from
our mechanical model.
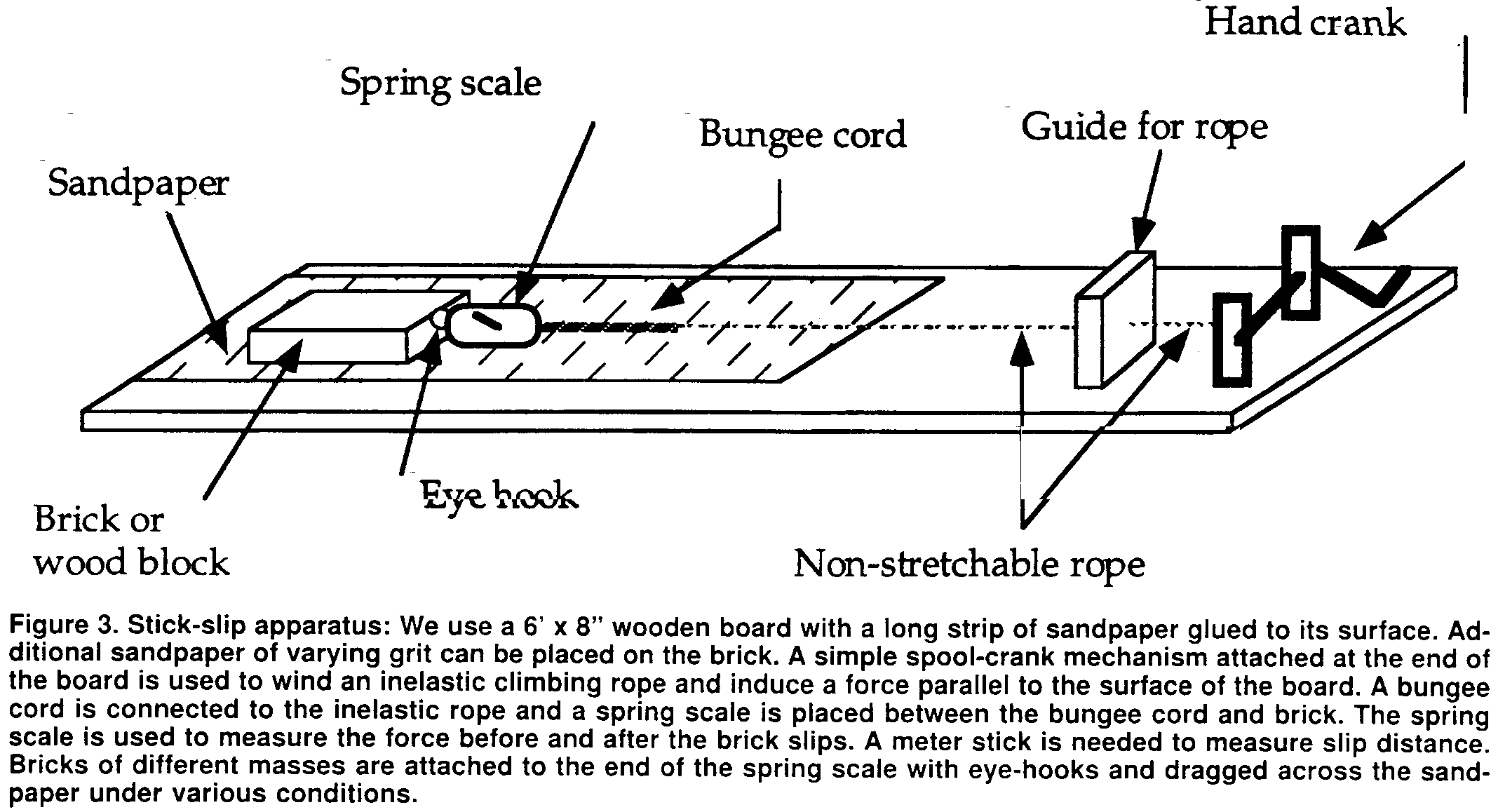
The earthquake cycle is modeled by turning the winch, stretching the bungee cord, and thereby placing a horizontal shear force on the fault. The bungee cord stores elastic strain energy in the system much as crustal rocks do to accommodate plate motion. Static friction proportional to the normal stress on the fault works against the horizontal force to hold the brick in place. In general, no slip occurs on the fault until a critical value of shear stress, t1, is reached; then, sudden slip occurs followed by a drop in shear stress to t2. After each slip event, a period of no slip ("stick") occurs during which the stress builds again to the critical value and the sudden slip is repeated.
The Experiment
In the following section, I will first describe the use of the experiment for teacher education and then discuss its modification for use with secondary-school students. Prior to conducting this experiment, in my Earth Hazards class for teachers, we discuss the elastic, brittle, and plastic behavior of rocks and the mechanics of fault rupture, friction, and plate motion. Additionally, we review the models for earthquake prediction and examine recurrence patterns on well documented faults. To introduce the experiment, the teachers are presented with a table full of materials they might need and are given the following instructions:
Given the materials on the front table, develop a model of fault behavior and determine what variables in the earth might affect the number or magnitude of earthquakes that occur. You might begin by thinking about how rocks behave, and about the driving force of earthquakes. In testing your model, you will need to investigate multiple variables in the earth-fault system and how you might model them. Keep detailed records of your experimental procedure, observations, and data. Develop physical or mathematical relationships that explain your observations, where possible. Show charts, graphs, and the analysis of your data.
Questions and ideas you might want to investigate in your group:
Few K-12 teachers have had much experience in designing experiments or exploring problems driven by curiosity. In this activity, their curiosity is stimulated by the knowledge that this is a real, unsolved research problem. The purpose of the activity is for them to design their own experiment and experience science as inquiry. Once assured that this is not a test, the teachers set to work with real enthusiasm. Groups are assigned so that each has a mixture of earth-science and physics teachers in hope that the physics teachers will recognize the classic friction experiment involved and that the earth-science teachers will lead the group in applying the laws of physics to the earth. The experiment is very open-ended, with multiple variables to be tested, including the inclination of the fault surface, the mass of the slider-block, the coefficient of friction, and the elastic behavior of the bungee cord.
Initially, many groups do not understand the role of the bungee cord in the model or which observations to measure and record. I encourage the teachers to discuss the experiment among the groups and to exchange ideas. Most groups recognize the gravitational force across the fault as an important component in their experiment, with the force being affected by both the mass of the brick and the inclination of the board. Typically, after one hour, most groups have correctly assembled the instrumentation, have a good idea of the variables they need to test, and are gathering data. After each group has investigated t least one variable, I initiate a discussion of what they have learned and accomplished so far using the questioning strategy of Penick and others (1996). The questions help the teachers identify differences in procedures among the groups and make adjustments to improve their experimental methods.
With just a few results, the teachers begin to recognize patterns in the data and the different effects of the variables. Some of the teams divide the task of testing variables between team members and are able to complete most of the data gathering by the end of the lab period. Each teacher is responsible for evaluating his/her own group’s data, predicting relationships, and drawing conclusions. The three-hour lab session in our short summer workshop is not long enough for each group to completely investigate the full problem. Rather than working in parallel, each group could take responsibility for investigating a particular variable and the data could be shared among the groups.
Modifying the Experiment for Secondary-School Classrooms
As a follow-up assignment, the teachers were required to modify the lab for use in their classrooms. Curiously, most teachers designed the activity to include very specific instructions on how to build the instrumentation and what to measure and record, thereby removing the joy of pure experimentation from the exercise. Discussions with the teachers revealed two reasons for this change: 1) the teacher did not think the students could do the activity without more structure, and/or 2) the more structured activity was similar to what the teachers were already doing in friction experiments and thus was more easily introduced into the curriculum. To determine if this activity could really work in a secondary-school classroom, I needed to learn more about the teachers, their students, and the constraints on teaching in K-12 classrooms. I have worked with two teachers to do this experiment in their classroom. In one classroom, junior- and senior-level physics students investigated fault behavior using a similar but more structured activity that was designed by the teacher. In the week prior to the activity, the teacher had reviewed basic concepts about earthquakes to prepare them for the experiment. At the beginning of the activity, the students were given specific instructions on how to construct the model, what to measure and how to analyze the data. The activity was completed in 50 minutes – a typical class period. Student-generated questions focused on the instructions and whether they were doing the experiment correctly. Discussions about the experiment and results were limited and difficult to stimulate. It was clear the students had not given much thought to the scientific method, the interpretation of the results, or the application of this experiment to the real Earth. The richness of the learning experience was lost to expediency and structure.
In the second classroom, I worked with ninth-grade earth-science students for 90 minutes. We used the more open-ended exercise described in this paper but shortened it by interweaving more class discussion to guide the activities. The exploration phase and building of the model lasted about 15 minutes. This was followed by a discussion of the variables involved in the experiment and the students’ initial understanding of how those variables might influence fault behavior. I divided the students into groups and allowed each group to choose a variable to investigate. All of the groups had sufficient time to investigate their variable; however, some did a much better job than others. Many groups needed help deciding what to record and how many measurements were needed to account for error and variability in the data. The student-generated questions focused less on the instructions and more on experiment design, data collection, and the behavior of faults. If there had been more time, I would have let them explore those questions more on their own rather than giving them hints and advice. Near the end of the class period, each group was asked to present its results and interpret them in terms of earthquake prediction. The presentations were quite promising. More sophisticated groups had graphed their data and calculated basic statistics. Other groups had generalized their observations qualitatively. In all cases, the students arrived at reasonable interpretations of their data and had genuine insight into fault behavior and earthquake prediction.
I continue to work with several teachers to design a still open-ended but more structured lab for secondary-school students. In the classroom with the earth-science students, it was apparent that secondary-school students need more structure in the activity but not in the form of instructions. Rather, the students have shorter attention spans and the activity therefore needs to be broken into smaller segments with more discussion and analysis intermixed to keep them interested and on task. Alternatively, this project could be extended over several weeks with a mixture of in-class and homework assignments that develop the scientific background necessary for the students to thoroughly investigate fault behavior and earthquake prediction (for example, see Conn, 1995).
Data Analysis and Evaluation of the Models
Data gathering and analysis will vary from student to student depending on understanding of the problem, curiosity, and initiative. In defining the assignment, I suggested questions the teachers should investigate in the experiment but specified neither how to investigate them nor what to do in gathering and analyzing the data. Most of the analysis can be done by applying simple statistics and graphing the data using a spreadsheet. In Table 1 and Figures 4-7, I present some of the data and analysis from experiments in which I varied: 1) the mass of the brick to simulate changes in lithostatic stress or overburden and 2) the coarseness of the sandpaper to reflect changes in friction and asperities. Each test was repeated 50 times to gather enough data for statistical analysis and to demonstrate the variability in slip behavior.
Basic data analysis can begin with a calculation of the minimum,
maximum, mode and median values of fi, fr, (fr-fi), and slip.
The data in Table 1 reveal an increase in average fi and slip
with an increase in the mass of the brick or coarseness of the
sandpaper. The largest slip event occurs with the heavier brick
and coarser sandpaper. To determine the cause of an increase in
number or magnitude of earthquakes, I compared the average and
maximum slip for the different experiments. For the same amount
of total slip, a smooth fault with low overburden will have nearly
three times as many earthquakes as a rough fault with greater
overburden. However, the rough fault has the potential for earthquake
with more than twice as much slip (Table 1).

More advanced statistics may include calculating a linear regression and correlation coefficient for the relationships between fi and slip and (fi-fr) and slip. An x-y plot of (fi-fr) and slip clearly reveals that a positive linear correlation exists for all cases (Figure 4). However, there is no correlation between fi and slip. Both of those results are consistent with observations of real faults in which slip is proportional to stress drop on the fault.
We can calculate the stress at the initiation and cessation
of slip using fi and fr, respectively, for each even t and then
construct a stress history similar to those in the theoretical
models for earthquake prediction (Figure 2). The time variable
is not easily controlled in the mechanical model. The best approximation
of time is to relate it to the amount of string coiled on the
winch and assume that plate motion is constant. However, in comparing
the theoretical models for earthquake prediction to the results
from the mechanical models, it is sufficient to focus on the stress
history independent of time.

Figures 5 and 6 show the stress histories for the 50 slip events
recorded for each model in Table 1. Each slip event is represented
by two points, t1 and t2, the shear stress at slip initiation
and cessation, respectively. The buildup and relaxation of stress,
and the great variability in the behavior of the stick-slip model
under different conditions, are readily apparent. None of the
data sets is identical to the end-member earthquake-prediction
models in Figure 2, but aspects of at least one model are visible
in most experiments. All of the data sets from the mechanical
models exhibit some "characteristic" slip behavior over
at least three earthquake cycles. In Figure 5a, the results for
a smooth fault with a low overburden are shown. For events 67-72,
the fault slip initiates at the same high shear stress t1 and
ceases at the lower shear stress t2 as expected with the characteristic
earthquake model, but there is little evidence for slip- or time-predictable
behavior. There is also a change in the variability of stress
drop and slip with increasing numbers of earthquakes, which suggests
that smoothing of the fault over time takes place.
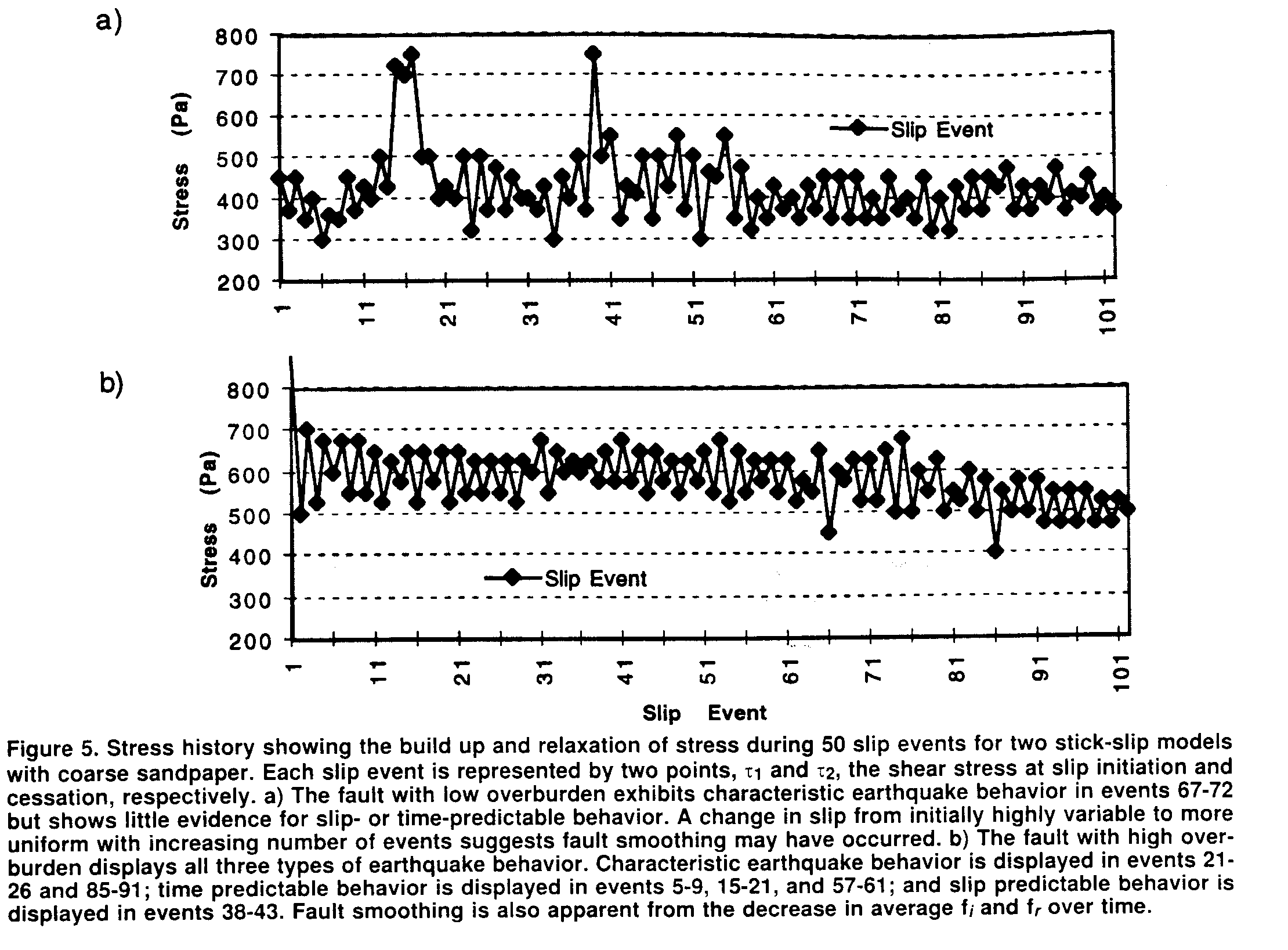
The mechanical model of a smooth fault with high overburden
displays all three types of fault behavior (Figure 5b). Characteristic
behavior is displayed in events 21-26 and 85-91. Time-predictable
behavior, in which the fault always slips at the same t1, is displayed
in events 5-9, 15-21, and 57-61. Slip-predictable behavior, in
which shear stress always relaxes to the same t2, is displayed
in events 38-43. Fault smoothing is evident in the decrease in
t1 and t3 with increasing number of slip events. A mechanical
model of a rough fault with low overburden displays all three
types of fault behavior as well. In Figure 6a, characteristic
behavior is shown in events 86-91, time-predictable behavior is
shown in events 62-71. The least predictable mechanical model
is the rough fault with high overburden (Figure 6b). Although
this model displays characteristic behavior in events 48-53, there
is no other sequence of slip events which supports earthquake
predictability.

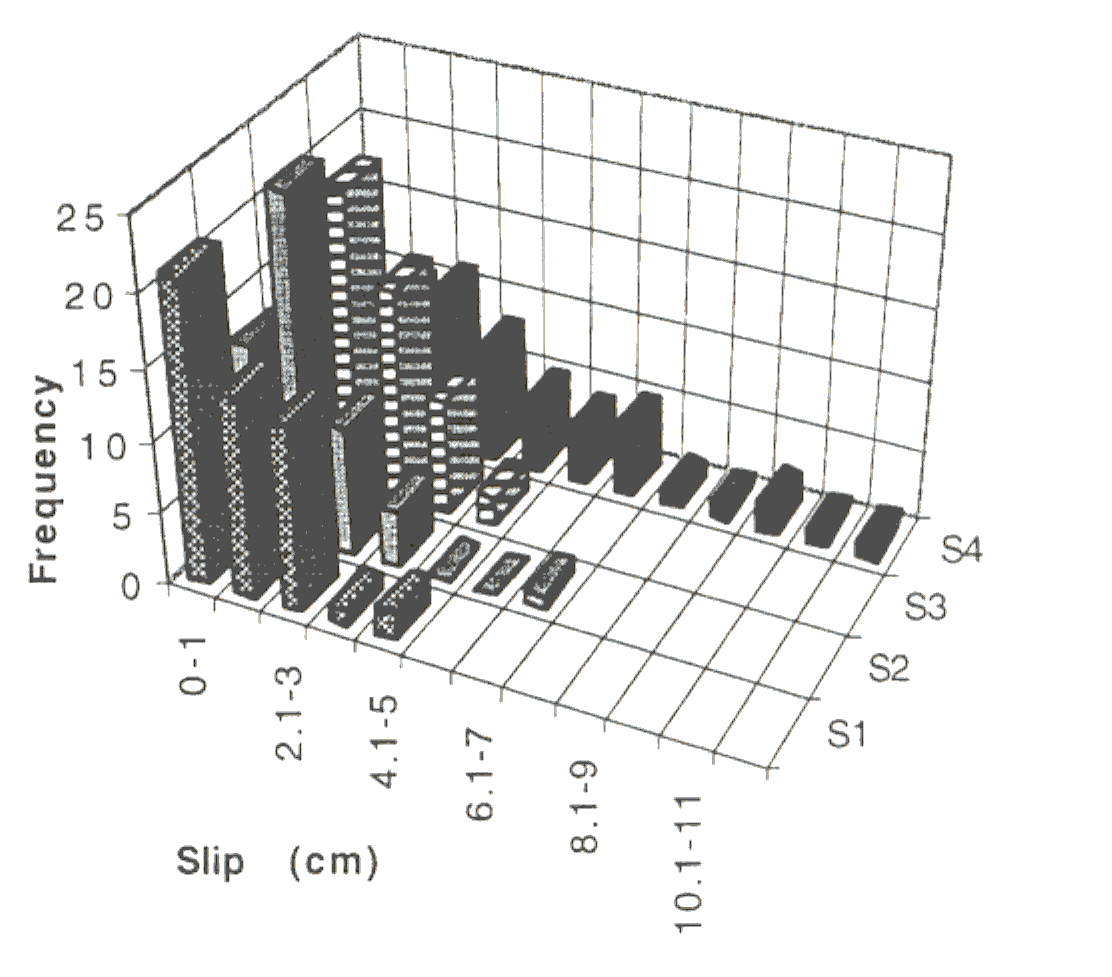
A plot showing the frequency of different size (magnitude) slip events (Figure 7) corresponds well with observations of real faults. In all models, there is a much higher frequency of small to moderate slip events than of very large and very small events. In the stick-slip model, as for real faults, the number of small events reflects the difficulty in detecting and recording them. The smaller number of large events is expected because large events release more strain energy and require more time to build up that strain energy before rupture.
Finally, each mechanical model had five events (10%) with more than twice the average slip for that particular model. This suggests there may be a statistical basis for predicting the size of the larger earthquakes expected on a fault. These results are consistent with observations of real faults which show similar variability in slip and do not fit nicely into any one category of slip behavior (Figure 2). The important point to remember in analyzing data from this experiment is that we rarely have a comparable about of earthquake-recurrence information for real faults. Often we have records of just one or two major earthquakes in the past, and they may indicate either that a fault has quite predictable behavior, or just the opposite. Therein lies a major problem in earthquake prediction on real faults.

The elastic behavior of the bungee cord was the most difficult variable to evaluate in the experiment because the relationship between rock type and bungee cord elasticity is not straightforward. There is a strong trade-off in stick-slip behavior between the elasticity of the bungee cord, the mass of the brick, and the coefficient of friction. Weak bungee cords with a lower sliding-block mass and smooth sandpaper provide the most stick-slip-like behavior. A weak bungee cord with a high –mass block and coarse sandpaper or a strong bungee cord with a low-mass block and smooth sandpaper results in creep-like behavior directly proportional to the shortening of the rope around the winch. In contrast, a high-mass block with coarse sandpaper and a strong bungee cord results in fewer, larger slip events.
We concluded our experiment with a discussion of the basic relationships shown by the data and how they apply to real earthquakes. In addition, we reviewed the lab procedures used and tried to identify ways they might be improved for better analysis. The quantitative and qualitative assessments students made highlighted the difficulty of predicting earthquakes even in a controlled laboratory experiment. In the end, the students realized that no single variable controls earthquake magnitude and the number of earthquakes and that the earth is a complex system.
Conclusions
Although the slider-block model cannot fully represent the complexity of the real Earth, the data and observations from the experiment illustrate quite well the general behavior of faults and the difficulty of predicting earthquakes . A variation of the fault model which includes two brick s in a series separated by a short bungee cord was demonstrated at the end of the lab to illustrate the complex interaction between segments on a major fault as one segment triggers slip on the other.
The skills and knowledge gained in this activity go beyond an increased understanding of fault behavior and earthquake prediction. This activity provides a unique opportunity for students to design their own experiments and develop skills vital to scientific literacy or a career in science. Students learn science by doing science and reinforce their ability to use scientific reasoning to solve problems. In addition, the experiment provides many opportunities for data gathering, plotting and analysis, and determining the value of the data in developing a model of earthquake prediction, or any other phenomenon. Unlike an activity in which the procedure and analysis are specified in advance, students will discover first hand the variables in their experiment and the value and limitations of their model.
In course evaluations and informal discussions, teachers indicated that this experiment was the highlight of the summer workshop because of its open-ended structure and the opportunity for them to design their own experiments. One teacher summarized his experience with these comments: "I thoroughly enjoyed the openness of this activity because it has no definitive answers. Data can be obtained and formulated into a hypothesis. Once the hypothesis has been reached, it can be researched in the lab or library to determine which methods [of earthquake prediction] are in use, have been attempted, or possibly could be used in the future as earthquake prediction systems."
Acknowledgments
This activity arose from discussions with Ross Stein about a model he developed to demonstrate earthquake behavior. The model and activity were refined after discussions with Ross Stein, Terry Wallace and George Zandt. A special thanks to the many students and teachers who have taught me so much about teaching. The paper was improved by constructive reviews from Meredith Nettles, Terry Wallace, Susan Beck, George Zandt and two anonymous reviewers. Southern Arizona Seismic Observatory contribution number 104.
References
Bakun, W.H., and Lindh, A.G., 1985, The Parkfield, California, earthquake prediction experiment: Science, v. 229, no. 4714, p. 619-624.
Brace and Byerlee, 1967, Recent experimental studies of brittle fracture in rocks, in C. Fairhurst, Editor, Failure and breakage of rock: Proceedings of the Eighth Symposium on Rock Mechanics, University of Minnesota, 1966, p. 58-81.
Bufe, C.G., Harsh, P.W., and Durford, R.O., 1977, Steady state seismic slip – A precise recurrence model: Geophysical Research Letters, v. 4, p. 91-94.
Byerlee, J.D., 1967, Frictional characteristics of granite under high confining pressure: Journal of Geophysical Research, v. 72, p. 3639-3648.
Coleman, S.L. and Soellner, A.M., 1995, Scientific literacy and earthquake prediction: Journal of Geological Education, v. 43, p. 147-151.
Conn, K., 1995, Engineering student success: The Science Teacher, v. 62, no. 6, p. 26-29.
Evans, D.M., 1966, Man-made earthquakes in Denver: Geotimes, v. 10, no. 9, p. 11-18.
Kanamori, H., 1977, The energy release in great earthquakes: Journal of Geophysical Research, v. 82, p. 2981-2987.
Lay, T., and Wallace, T.C., 1995, Modern global seismology: Academic Press, San Diego, California, p. 521.
Marone, C., and Scholz, C.H., 1988, The depth of seismic faulting and the upper transition from stable to unstable slip regimes: Geophysical Research Letters, v. 15, p. 621-624.
National Research Council, 1996, National Science Education Standards: National Academy of Science Publishing, Washington DC, p. 262.
Penick, J.E., Crow, L.W., Bonnstetter, R.J., 1996. Questions are the answer: The Science Teacher, v. 63, no. 1, p. 27-29.
Picard, M.D., Earthquake news: Journal of Geological Education, v. 43, p. 542-547.
Reid, H.F., 1910, The mechanics of the California earthquake of April 18, 1906: Report of the State Earthquake Investigative Committee, Washington DC, Carnegie Institute.
Scholz, C.H., 1990, The mechanics of earthquakes and faulting: Cambridge University Press, New York, NY, p. 438.
Shimazaki, K., and Nakata, T., 1980, Time-predictable recurrence model for large earthquakes: Geophysical Research Letters, v. 7, p. 279-282.
Simpson, D.W., Leith, W.S., and Scholz, C.H., 1988, Two types of reservoir induced seismicity: Bulletin of the Seismological Society of America, v. 78, p. 2025-2040.
Wallace, M.H., and Kemeny, J., 1992, Nucleation and growth of dip-slip faults in a stable craton: Journal of Geophysical Research, v. 97, no. B5, p. 7145-7157.
Wallace, M.H., and Wallace, T.C., 1993, The paradox of the Loma Prieta earthquake: Why did rupture terminate at depth?: Journal of Geophysical Research, v. 98, no. B11, p. 19,859-19,867.
Walsh, J., and Watterson, J., 1988, Analysis of the relationship
between displacements and dimensions of faults: Journal of Structural
Geology, v. 10, p. 238-247.
About the Author
Michelle Hall-Wallace is an assistant professor in the Department of Geosciences at the University of Arizona. She received her BS degree in geological engineering from the South Dakota School of Mines and Technology and her MS and PhD in geophysics from the University of Arizona. Her interests include geologic hazards, developing computer/mathematics based curriculum materials and working to make science relevant and accessible to all students.
Created By Dave Love, Chris Durand and John Van Der Kamp
last modified: 25 April, 2022